프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제 설명
두 수의 최소공배수(Least Common Multiple)란 입력된 두 수의 배수 중 공통이 되는 가장 작은 숫자를 의미합니다. 예를 들어 2와 7의 최소공배수는 14가 됩니다. 정의를 확장해서, n개의 수의 최소공배수는 n 개의 수들의 배수 중 공통이 되는 가장 작은 숫자가 됩니다. n개의 숫자를 담은 배열 arr이 입력되었을 때 이 수들의 최소공배수를 반환하는 함수, solution을 완성해 주세요.
제한사항
- arr은 길이 1 이상, 15 이하인 배열입니다.
- arr의 원소는 100 이하인 자연수입니다.
입출력 예
| arr | result |
| [2,6,8,14] | 168 |
| [1,2,3] | 6 |
풀이
오늘도 추억에 빠질 시간입니다. 풀이 방법은 여러 가지가 있는데 그중 유클리드 호제법에 대해 설명하려고 합니다.
class Solution {
fun solution(arr: IntArray): Int {
var answer = 0
for(i in 0 until arr.size-1){
arr[i+1] = (arr[i] * arr[i+1]) / getMin(arr[i], arr[i+1])
}
return arr[arr.size-1]
}
fun getMin(a: Int, b: Int): Int{
var a = a
var b = b
var temp = 0
while(true) {
temp = b % a
b = a
a = temp
if(temp == 0)
return b
}
}
}코드는 다음과 같습니다. getMin() 함수가 최대 공약수를 구하는 함수입니다.
유클리드 호제법, 익숙하지만 기억 안 납니다. 검색해보니 초등학교 5학년 때 배웠던 개념이더라고요. 정의는 다음과 같습니다.
두 양의 정수 a, b (a> b)에 대하여 a = bq + r (0 <= r < b)이라 하면, a, b, 의 최대공약수는 b, r의 최대공약수와 같다. 즉, gcd(a, b) = gcd(b, r) / r = 0이라면 a, b의 최대공약수는 b가 된다.
라는 정의입니다. (gcd = Greatest Common Divisor, 최대공약수)
정의도 알았고 알고리즘도 어떻게 짜야할지 알았습니다. 이제 이게 왜 성립하는지 증명해봅시다.
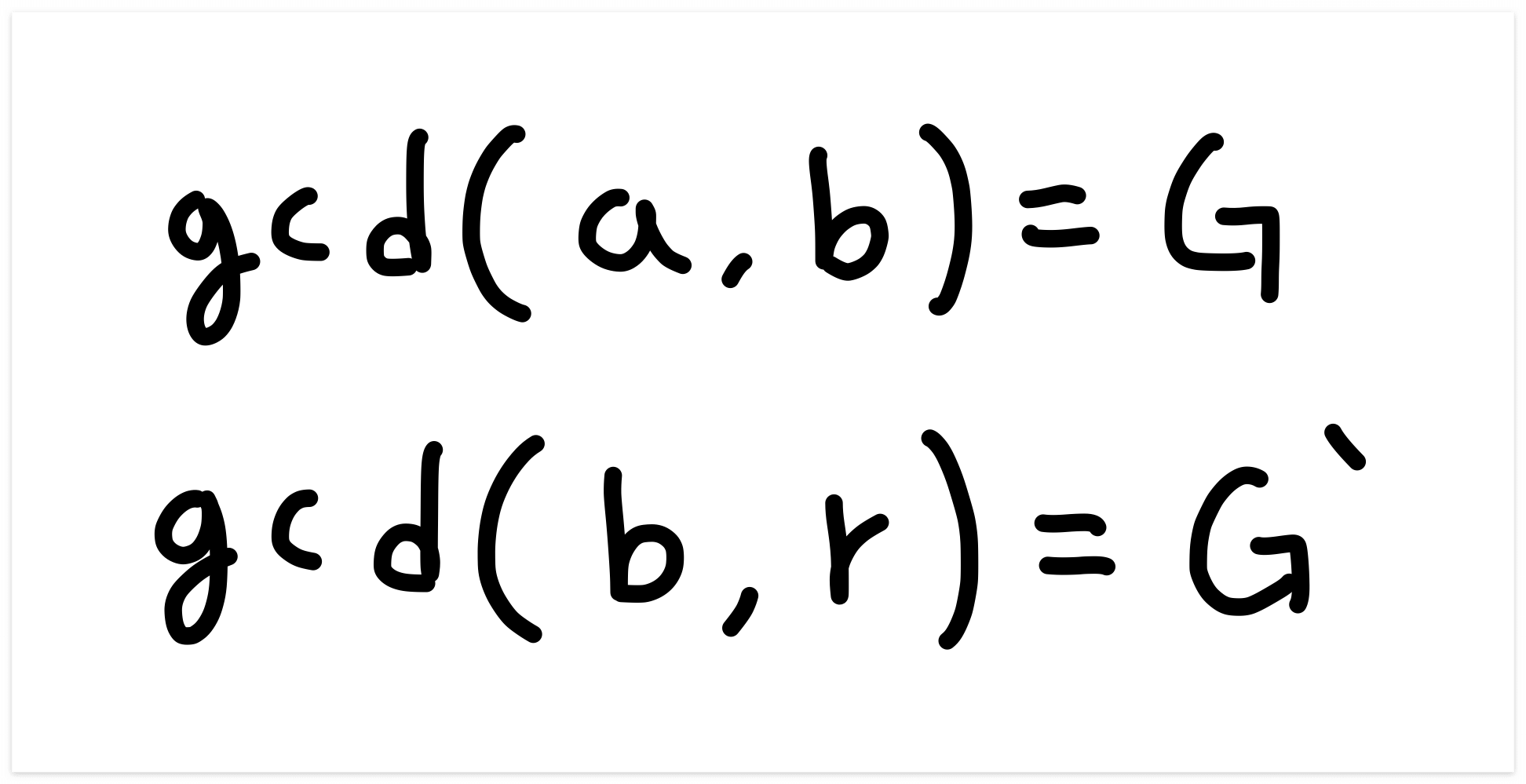
a와 b의 최대 공약수를 G, b와 r의 최대 공약수를 G`라고 가정해봅시다. a와 b는 최대공약수 G * 서로소입니다. 따라서 적당한 서로소인 정수 A, B를 대입하면 아래와 같이 나옵니다.

이를 정의에 나왔던 a = bq + r에 대입해봅시다.

대입 결과 G는 r의 약수이고 따라서 b와 r의 공약수인 것을 알 수 있습니다. 즉, G는 b와 r의 최대공약수 G`의 약수입니다.
G` = mG로 두고 적당한 서로소 k, l를 G`에 곱해봅시다.
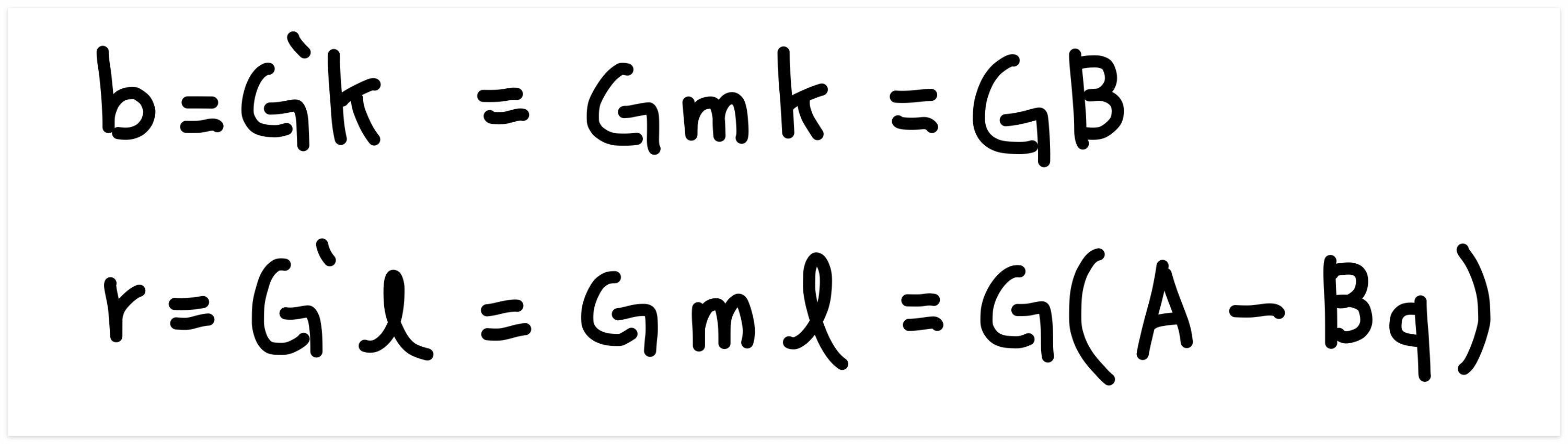
두 식 모두 양변에 G를 나누면

B = mk, A = ml + Bq 식을 얻을 수 있습니다. A 식에 B를 대입해주면

A = m(l + kq) 임을 알 수 있습니다. m은 A와 B의 공약수인데 서로소의 최대공약수는 항상 1이므로 따라서 m = 1이고 G = G`임을 알 수 있습니다.
후기
사실 이전에 비슷한 문제를 2번이나 풀어본 적 있어서 유클리드 호제법과 상관없이 기계적으로 풀었습니다. 처음 풀 때만 해도 못 풀어서 식을 외워버렸는데 이제야 제대로 된 정의와 증명을 해보네요. 시간이 갈수록 확률, 통계 쪽을 공부해봐야겠다는 생각이 듭니다.
다른 사람의 풀이
class Solution {
fun solution(arr: IntArray): Int {
var answer = 1
while(true) {
var x = 0
for(a in arr) x += answer%a
if(x==0) return answer
answer++
}
return answer
}
}유클리드 호제법만이 이 문제의 풀이는 아닙니다. 반복문과 조건문을 이용해서 주어진 모든 수로 나눠 떨어지는 최소 공배수를 1부터 ∞까지 찾아나가면 됩니다.
출처
쉽게 설명돼있는 게 나무 위키라 별수없이 가져왔습니다.
유클리드 호제법 - 나무위키
손으로 계산할 때는 제수와 피제수의 값 크기를 비교해서 적절하게 배열하지만 수식이나 코드로 나타낼 때는 신경쓰지 않아도 되는데, a일 때 a mod b ≡ a(a%b==a)이므로 Gcd(a,b)는 Gcd(b,a)를 호출한다
namu.wiki
약수 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 수론에서 약수(約數, 영어: divisor) 또는 인수(因數, 영어: factor, 전 용어: 승자(乘子))는 어떤 수를 나누어떨어지게 하는 수를 말한다. 다항식의 약수나 가환환의
ko.wikipedia.org
'코딩테스트 > 프로그래머스' 카테고리의 다른 글
| H-Index(Lv.2) (0) | 2022.09.26 |
|---|---|
| 예상대진표(Lv.2) (1) | 2022.09.21 |
| 멀리 뛰기(Lv.2) (0) | 2022.09.19 |
| 피보나치 수(Lv.2) (0) | 2022.09.18 |
| 이진변환 반복하기(Lv.2) (0) | 2022.09.16 |
